거의 알고리즘 일기장
백준 11266번 _ 단절점 본문
https://www.acmicpc.net/problem/11266
11266번: 단절점
첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B가 주어진다. 이는 A번 정점과 B번 정점이 연결되어 있다는 의미이며, 방향은 양방향이다. 입력으로 주어지는 그래프는 연결 그래프가 아닐 수도 있다.
www.acmicpc.net
1. 풀이방법
그래프의 단절점 알고리즘의 기본적인 연습문제이다.
단절점을 찾는 방법을 예시로 들면
ex)
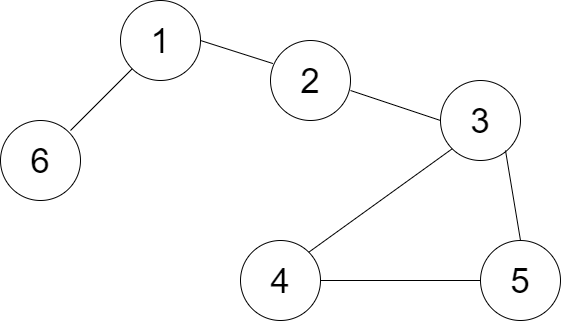
1) dfs스패닝 트리를 만든다. ( 찾은 순서를 기록한다 )
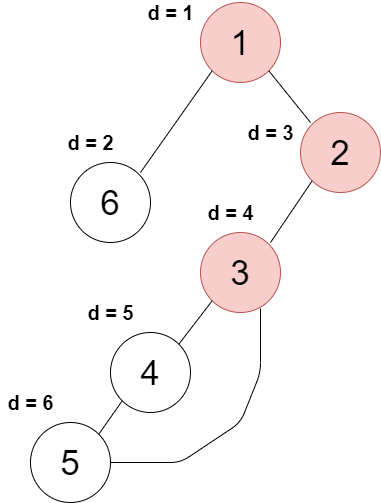
2) 각 정점에서의 역방향간선을 한번 이용하여 갈수있는 d가 가장 작은 노드의 d값 ( L이라고 하겠음 ) 을 구한다.
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 |
| d | 1 | 3 | 4 | 5 | 6 | 2 |
| L | 1 | 1 | 3 | 4 | 4 | 1 |
3) 인접한 두 정점을 비교한다 ( 루트인 정점 1은 따로 )
ex) 정점 2와 3 비교할때 d[2] = 3, L[3] = 3이므로
3번노드가 역방향 간선을 이용해서 가장 높게 갈수있는 곳이 2번노드 ( d[2] = 3 ) 이기 때문에
2번 정점을 없앴을때, 3번이 1번으로 갈수있는 경우는 없다.
그러니 정점 2번은 단절점이다. ( 밑의 그림 참고 )
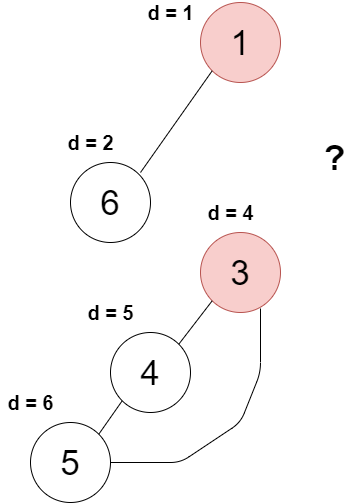
그 외에 루트가 단절점인지 아닌지를 확인할때는 그냥 자식노드가 몇개인지만 알면 된다.
자식노드 1개 -> 단절점 x
자식노드 2개 이상 -> 단절점
2. 코드
#include <iostream>
#include <algorithm>
#include <vector>
#define MAXV 10002
using namespace std;
int v, e;
vector<vector<int>> adj;
int discovered[MAXV];
bool visit[MAXV];
int cnt = 0;
bool cutPoint[MAXV];
int dfs(int here, bool isRoot)
{
discovered[here] = ++cnt;
int child = 0;
int ret = discovered[here];
for (int i = 0; i < (int)adj[here].size(); i++)
{
int there = adj[here][i];
if (discovered[there] == 0)
{
child++;
int subtree = dfs(there, false);
//절단점
if (!isRoot && subtree >= discovered[here])
{
cutPoint[here] = true;
}
ret = min(ret, subtree);
}
//역방향 간선일때
else
{
ret = min(ret, discovered[there]);
}
}
//루트일때
if (isRoot && child > 1)
cutPoint[here] = true;
return ret;
}
int main()
{
cin >> v >> e;
adj.resize(v + 2);
//make adj, 양방향 간선임
int first, second;
int maxNode = 0;
for (int i = 0; i < e; i++)
{
cin >> first >> second;
adj[first].push_back(second);
adj[second].push_back(first);
maxNode = max(maxNode, first);
maxNode = max(maxNode, second);
}
for (int i = 1; i <= maxNode; i++)
{
if(discovered[i] == 0)
dfs(i, true);
}
vector<int > result;
for (int i = 1; i <= maxNode; i++)
if (cutPoint[i] == true)
result.push_back(i);
cout << result.size() << '\n';
for (auto& ele : result)
cout << ele << ' ';
return 0;
}
3. 후기
단절점에 대해서는 안다고 생각했는데 막상 설명하려니 헷갈리고 그랬다.
그래서 그런지 이 글은 처음보는 사람이 이해하기란 매우 어려울것 같다...
나중에 보완해야겠다.
'알고리즘 문제풀이' 카테고리의 다른 글
| 백준 9172 _ 상근이의 여행 (0) | 2020.04.04 |
|---|---|
| 백준 14002번 _가장 긴 증가하는 부분 수열 4 (0) | 2020.04.04 |
| 프로그래머스 _ 순위 (0) | 2020.04.04 |
| 프로그래머스 _ 가장 먼 노드 (0) | 2020.04.04 |
| 백준 1956번 _ 운동 (0) | 2020.04.03 |
